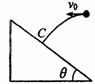
如图所示,在半径为R,质量分布均匀的某星球表面,有一倾角为θ的斜坡。以初速度v0向斜坡水平抛出一个小球。测得经过时间t,小球垂直落在斜坡上的C点。
求:(1)小球落到斜坡上时的速度大小v;
(2)该星球表面附近的重力加速度g;
(3)卫星绕该星球表面做匀速圆周运动的速度![]() 。
。
答案
解(1)由速度的合成与分解图可知![]()
 求出
求出 ![]()
(2)由图可知 ![]()
![]() =gt
=gt
求出 ![]()
(3)根据 ![]()
求出 ![]()
如图所示,在半径为R,质量分布均匀的某星球表面,有一倾角为θ的斜坡。以初速度v0向斜坡水平抛出一个小球。测得经过时间t,小球垂直落在斜坡上的C点。
求:(1)小球落到斜坡上时的速度大小v;
(2)该星球表面附近的重力加速度g;
(3)卫星绕该星球表面做匀速圆周运动的速度![]() 。
。

解(1)由速度的合成与分解图可知![]()
 求出
求出 ![]()
(2)由图可知 ![]()
![]() =gt
=gt
求出 ![]()
(3)根据 ![]()
求出 ![]()