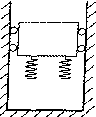
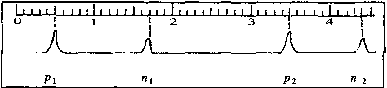
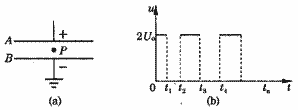
如图（ａ）所示，Ａ、Ｂ为水平放置的平行金属板，板间距离为ｄ（ｄ远小于板的长和宽）．在两板之间有一带负电的质点Ｐ．已知若在Ａ、Ｂ间加电压Ｕ_o，则质点Ｐ可以静止平衡．现在Ａ、Ｂ间加上如图（ｂ）所示的随时间ｔ变化的电压ｕ．在ｔ＝0时质点Ｐ位于Ａ、Ｂ间的中点处且初速为零．已知质点Ｐ能在Ａ、Ｂ之间以最大的幅度上下运动而又不与两板相碰，求图（ｂ）中ｕ改变的各时刻ｔ_１、ｔ_２、ｔ_３及ｔ_ｎ的表达式．（质点开始从中点上升到最高点，及以后每次从最高点到最低点或从最低点到最高点的过程中，电压只改变一次．）

解：设质点Ｐ的质量为ｍ，电量大小为，根据题意，当Ａ、Ｂ间的电压为时，有

／ｄ＝ｍｇ，
当两板间的电压为2Ｕ_０时，Ｐ的加速度向上，其大小为ａ，则
（ｑ2／ｄ）－ｍｇ＝ｍａ，
解得ａ＝ｇ．
当两板间的电压为零时，Ｐ自由下落，加速度为ｇ，方向向下．
在ｔ＝0时，两板间的电压为2，Ｐ自Ａ、Ｂ间的中点向上做初速度为零的匀加速运动，加速度为ｇ．设经过时间τ_１，Ｐ的速度变为，此时使电压变为零，让Ｐ在重力作用下做匀减速运动，再经过时间τ_１′，Ｐ正好到达Ａ板且速度为零，故有
＝ｇτ_１，0＝－ｇτ_１′，
（1／2）ｄ＝（1／2）ｇτ_１^２＋τ_１′－（1／2）ｇτ_１′^２，
由以上各式，得
τ_１＝τ_１′，τ_１＝（／2），
因为ｔ_１＝τ_１，得ｔ_１＝（／2）．
在重力作用下，Ｐ由Ａ板处向下做匀加速运动，经过时间τ_２，速度变为ｖ_２，方向向下，这时加上电压使Ｐ做匀减速运动，经过时间τ_２′，Ｐ到达Ｂ板且速度为零，故有
ｖ_２＝ｇτ_２，0＝ｖ_２－ｇτ_２′，
ｄ＝（1／2）ｇτ_２^２＋ｖ_２τ_２′－（1／2）ｇτ_２′^２，
由以上各式，得τ_２＝τ_２′，τ_２＝，
因为ｔ_２＝ｔ_１＋τ_１′＋τ_２，
得ｔ_２＝（＋1）．
在电场力与重力的合力作用下，Ｐ由Ｂ板处向上做匀加速运动，经过时间τ_３，速度变为ｖ_３，此时使电压变为零，让Ｐ在重力作用下做匀减速运动．经过时间τ_３′，Ｐ正好到达Ａ板且速度为零，故有
ｖ_３＝ｇτ_３，0＝ｖ_３－ｇτ_３′，
ｄ＝（1／2）ｇτ_３^２＋ｖ_３τ_３′－（1／2）ｇτ_３′^２
由上得τ_３＝τ_３′，τ_３＝，
因为ｔ_３＝ｔ_２＋τ_２′＋τ_３，
得ｔ_３＝（＋3）．
根据上面分析，因重力作用，Ｐ由Ａ板向下做匀加速运动，经过时间τ_２，再加上电压，经过时间τ_２′，Ｐ到达Ｂ且速度为零，因为ｔ_４＝ｔ_３＋τ_３′＋τ_２，
得ｔ_４＝（＋5）．

同样分析可得：ｔ_ｎ＝（＋2ｎ－3）．（ｎ≥2）