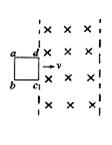
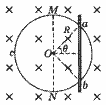
如图所示，半径为Ｒ、单位长度电阻为λ的均匀导体圆环固定在水平面上，圆环中心为Ｏ．匀强磁场垂直水平面方向向下，磁感强度为Ｂ．平行于直径ＭＯＮ的导体杆，沿垂直于杆的方向向右运动．杆的电阻可以忽略不计，杆与圆环接触良好，某时刻，杆的位置如图，∠ａＯｂ＝2θ，速度为ｖ，求此时刻作用在杆上安培力的大小．
解：如图所示，杆切割磁力线时，ａｂ部分产生的感应电动势
Ｅ＝ｖＢ（2Ｒｓｉｎθ），
此时弧ａｃｂ和弧ａｄｂ的电阻分别为2λＲ（π－θ）和2λＲθ，它们并联后的电阻为
ｒ＝2λＲθ（π－θ）／π，
杆中的电流为Ｉ＝Ｅ／ｒ，
作用在杆上的安培力为Ｆ＝ＩＢ（2Ｒｓｉｎθ），
由以上各式解得Ｆ＝（2πｖＢ２Ｒ／λ）（ｓｉｎ２θ／θ（π－θ））．
法拉第电磁感应定律：
（n为线圈匝数）。 
； 
。 导体切割磁感线的两个特例：
的区别与联系及选用原则：
电磁感应中动力学问题的解法：
电磁感应和力学问题的综合，其联系的桥梁是磁场对感应电流的安培力，因为感应电流与导体运动的加速度有相互制约的关系。
1．分析思路
(1)用法拉第电磁感应定律和楞次定律求感应电动势的大小和方向。
(2)求回路中的电流。
(3)分析研究导体受力情况(包含安培力，用左手定则确定其方向)。
(4)列动力学方程或平衡方程求解。
2．常见的动态分析这类问题中的导体一般不是做匀变速运动，而是经历一个动态变化过程再趋于一个稳定状态，故解这类问题时正确进行动态分析确定最终状态是解题的关键。同时也要抓好受力情况和运动情况的动态分析，研究顺序为：导体受力运动产生感应电动势一感应电流一通电导体受安培力一合外力变化一加速度变化一速度变化一周而复始地循环，循环结束时，加速度等于零．导体达到稳定运动状态。
电磁感应中的动力学临界问题：
(1)解决这类问题的关键是通过运动状态的分析，寻找过程中的临界状态，如速度、加速度求最大值或最小值的条件。
(2)基本思路：
登录并加入会员可无限制查看知识点解析
bcd
