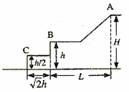
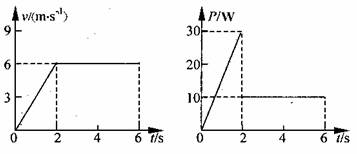
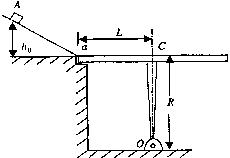
如图所示,光滑斜面的底端a与一块质量均匀、水平放置的平极光滑相接,平板长为2L,L=1m,其中心C固定在高为R的竖直支架上,R=1m,支架的下端与垂直于纸面的固定转轴O连接,因此平板可绕转轴O沿顺时针方向翻转.问:
(l)在外面上离平板高度为h0处放置一滑块A,使其由静止滑下,滑块与平板间的动摩擦因数μ=0.2,为使平板不翻转,h0最大为多少?
(2)如果斜面上的滑块离平板的高度为h1=0.45 m,并在h1处先后由静止释放两块质量相同的滑块A、B,时间间隔为Δt=0.2s,则B滑块滑上平板后多少时间,平板恰好翻转。(重力加速度g取10 m/s2)
答案
解:(1)设A滑到a处的速度为v0=![]() ①
①
f=uN,N=mg,f=ma, a=ug
滑到板上离a点的最大距离为v02=2ugs0,
s0=2gh0/2ug=h0/u ③
A在板上不翻转应满足条件:摩擦力矩小于正压力力矩,即M摩擦≤M压力
umgR≤mg(L-s0) ④
h0≤u(L-Ur)=0.2(1-0.2)=0.16 m ⑤
(2)当h=0.45m,vA=![]() =
=![]() =3m/s
=3m/s
vA=vB=3m/s ⑥
设B在平板上运动直到平板翻转的时刻为t,取Δt=0.2s
sA=vA(t+Δt)-ug(t+Δt)2/2 ⑦’
sB=vBt-ugt2/2 ⑦
两物体在平板上恰好保持平板不翻转的条件是
2umgR=mg(L-sA)+mg(L-sB) ⑧
由⑦+⑦’式等于⑧式,得t=0.2s


 满足
满足 时,物体可在轨道上速度减小到零,即动能可全部转化为重力势能;在
时,物体可在轨道上速度减小到零,即动能可全部转化为重力势能;在 ,物体上升到圆周最高点时的速度
,物体上升到圆周最高点时的速度 )时,物体可做完整的圆周运动;若在
)时,物体可做完整的圆周运动;若在 时,物体将在与圆心等高的位置与圆周最高点之间某处脱离轨道,之后物体做斜上抛运动,到达最高点时速度不为零,动能不能全部转化为重力势能,物体实际上升的高度
时,物体将在与圆心等高的位置与圆周最高点之间某处脱离轨道,之后物体做斜上抛运动,到达最高点时速度不为零,动能不能全部转化为重力势能,物体实际上升的高度 满足
满足 。故在解决这类问题时不能单从能量守恒的角度来考虑。
。故在解决这类问题时不能单从能量守恒的角度来考虑。