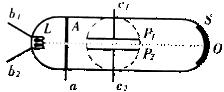
如图,两个共轴的圆筒形金属电极,外电极接地,其上均匀分布着平行于轴线的四条狭缝a、b、c和d,外筒的外半径为![]() 。在圆铜之外的足够大区域中有平行于轴线方向的均匀磁场,磁感强度的大小为B,在两极间加上电压,使两圆铜之间的区域内有沿半径向外的电场。一质量为m、带电量为+q的粒子,从紧靠内筒且正对狭缝a的S点出发,初速为零。
。在圆铜之外的足够大区域中有平行于轴线方向的均匀磁场,磁感强度的大小为B,在两极间加上电压,使两圆铜之间的区域内有沿半径向外的电场。一质量为m、带电量为+q的粒子,从紧靠内筒且正对狭缝a的S点出发,初速为零。
如果该粒子经过一段时间的运动之后恰好又回到出发点S,则两极之间的电压U应是多少?(不计重力,整个装置在真空中。)

答案
解:
带电粒子从S出发,在两筒之间的电场力作用下加速,沿径向穿出a而进入磁场区,在洛仑兹力作用下做匀速圆周运动。粒子再回到S点的条件是能沿径向穿过狭缝b。只要穿过了b,粒子就会在电场力作用下先减速,再反向加速,经b 重新进入磁场区。然后,粒子将以同样方式经过c、d,再经过a回到S点。

设粒子射入磁场区的速度为v,根据能量守恒,有: ![]() ①
①
设粒子在洛仑兹力作用下做匀速圆周运动的半径为R,由洛仑兹力公式和牛顿定律得
![]() ②
②
由前面分析可知,要回到S点,粒子从a到b必经过![]() 圆周,所以半径R必定等于筒的外半径
圆周,所以半径R必定等于筒的外半径![]() ,即:
,即: ![]() ③
③
由以上各式解得: ![]() ④
④