2019人教版(2019)高中物理单元测试138041
高中
整体难度：偏难
2020-12-14
题号
一
二
三
四
五
评分
一、解答题 (共20题)
添加该题型下试题
1.
静止在水平地面上的两小物块A、B，质量分别为
，
；两者之间有一被压缩的微型弹簧，A与其右侧的竖直墙壁距离
，如图所示．某时刻，将压缩的微型弹簧释放，使A、B瞬间分离，两物块获得的动能之和为
．释放后，A沿着与墙壁垂直的方向向右运动．A、B与地面之间的动摩擦因数均为
．重力加速度取
．A、B运动过程中所涉及的碰撞均为弹性碰撞且碰撞时间极短．
（1）求弹簧释放后瞬间A、B速度的大小；
（2）物块A、B中的哪一个先停止？该物块刚停止时A与B之间的距离是多少？
（3）A和B都停止后，A与B之间的距离是多少？
难度：
知识点：弹性碰撞和非弹性碰撞
使用次数：118
【答案】
（1）vA=4.0m/s，vB=1.0m/s；（2）B先停止； 0.50m；（3）0.91m；
【分析】
首先需要理解弹簧释放后瞬间的过程内A、B组成的系统动量守恒，再结合能量关系求解出A、B各自的速度大小；很容易判定A、B都会做匀减速直线运动，并且易知是B先停下，至于A是否已经到达墙处，则需要根据计算确定，结合几何关系可算出第二问结果；再判断A向左运动停下来之前是否与B发生碰撞，也需要通过计算确定，结合空间关系，列式求解即可．
【详解】
（1）设弹簧释放瞬间A和B的速度大小分别为vA、vB，以向右为正，由动量守恒定律和题给条件有
①
②
联立①②式并代入题给数据得
vA=4.0m/s，vB=1.0m/s
（2）A、B两物块与地面间的动摩擦因数相等，因而两者滑动时加速度大小相等，设为a．假设A和B发生碰撞前，已经有一个物块停止，此物块应为弹簧释放后速度较小的B．设从弹簧释放到B停止所需时间为t，B向左运动的路程为sB．，则有
④
⑤
⑥
在时间t内，A可能与墙发生弹性碰撞，碰撞后A将向左运动，碰撞并不改变A的速度大小，所以无论此碰撞是否发生，A在时间t内的路程sA都可表示为
sA=vAt–
⑦
联立③④⑤⑥⑦式并代入题给数据得
sA=1.75m，sB=0.25m⑧
这表明在时间t内A已与墙壁发生碰撞，但没有与B发生碰撞，此时A位于出发点右边0.25m处．B位于出发点左边0.25m处，两物块之间的距离s为
s=0.25m+0.25m=0.50m⑨
（3）t时刻后A将继续向左运动，假设它能与静止的B碰撞，碰撞时速度的大小为vA′，由动能定理有
⑩
联立③⑧⑩式并代入题给数据得
故A与B将发生碰撞．设碰撞后A、B的速度分别为vA′′以和vB′′，由动量守恒定律与机械能守恒定律有
联立
式并代入题给数据得
这表明碰撞后A将向右运动，B继续向左运动．设碰撞后A向右运动距离为sA′时停止，B向左运动距离为sB′时停止，由运动学公式
由④
式及题给数据得
sA′小于碰撞处到墙壁的距离．由上式可得两物块停止后的距离
2.
如图所示，质量M=4kg的滑板B静止放在光滑水平面上，其右端固定一根轻质弹簧，弹簧的自由端C到滑板左端的距离L=0.5 m，这段滑板与木块A（可视为质点）之间的动摩擦因数μ= 0.2，而弹簧自由端C到弹簧固定端D所对应的滑板上表面光滑．木块A以速度v0=10m/s由滑板B左端开始沿滑板B表面向右运动．已知木块A的质量m=lkg，g取10m/s2，．求：
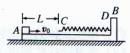
（1）弹簧被压缩到最短时木块A的速度
（2）木块A压缩弹簧过程中弹簧的最大弹性势能．
难度：
知识点：弹性碰撞和非弹性碰撞
使用次数：124
【答案】
（1）2 m/s；（2）39J.
【详解】
（1）弹簧被压缩到最短时，木块A与滑板B具有相同的速度，设为v，从木块A开始沿滑板B表面向右运动至弹簧被压缩到最短的过程中，A、B系统的动量守恒：
mv0＝（M＋m）v
解得v＝
v0
代入数据得木块A的速度v＝2 m/s
（2）木块A压缩弹簧过程中，弹簧被压缩到最短时，弹簧的弹性势能最大．
由能量关系，最大弹性势能Ep＝
mv02－（m＋M）v2－μmgL
代入数据得Ep＝39 J
3.
如图所示，一辆质量为M的小车静止在水平面上，车面上右端点有一可视为质点的滑块1，水平面上有与车右端相距为4R的固定的
光滑圆弧轨道，其圆周半径为R，圆周E处的切线是竖直的，车上表面与地面平行且与圆弧轨道的末端D等高，在圆弧轨道的最低点D处，有另一个可视为质点的滑块2，两滑块质量均为m．某人由静止开始推车，当车与圆弧轨道的竖直壁CD碰撞后人即撤去推力并离开小车，车碰后靠着竖直壁静止但不粘连，滑块1和滑块2则发生碰撞，碰后两滑块牢牢粘在一起不再分离．车与地面的摩擦不计，滑块1、2与车面的摩擦系数均为μ，重力加速度为g，滑块与车面的最大静摩擦力可认为等于滑动摩擦力．
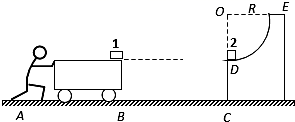
（1）若人推车的力是水平方向且大小为
，则在人推车的过程中，滑块1与车是否会发生相对运动？
（2）在（1）的条件下，滑块1与滑块2碰前瞬间，滑块1的速度多大？
（3）若车面的长度为
，小车质量M=km，则k的取值在什么范围内，两个滑块最终没有滑离车面？
难度：
知识点：弹性碰撞和非弹性碰撞
使用次数：100
【答案】
（1）滑块1与车面之间没有发生相对滑动；（2）
；（3）k≤2
【详解】
（1）设滑块1与车不发生相对滑动，加速度大小为a，由牛顿第二定律有：F=（M+m）a
此时滑块受到的静摩擦力大小为：f=ma
而：
联立解得：
又滑块1与车面的最大静摩擦力为：fm=μmg
显然f＜fm，说明滑块1与车面之间没有发生相对滑动．
（2）设滑块1与滑块2碰撞前瞬间滑块1的速度为v，根据动能定理有：
联立求得：
（3）设滑块1和2发生碰撞后的共同速度为v1，由动量守恒定律有：mv=2mv1
联立求得：
两滑块粘合在一起后以v1的速度冲上光滑圆弧轨道，由于圆弧轨道的E处的切线是竖直的，则无论两滑块在圆弧轨道上运动，还是从E处竖直向上离开圆弧轨道，最后还是沿着圆弧轨道回到D处，整个过程中两滑块的机械能守恒，两滑块最终以速度v1冲上车面．设两滑块滑到车的左端时，若滑块刚好不滑出车面，滑块和车应有共同的速度设为v2，由系统的动量守恒有：2mv1=（2m+km）v2，
由系统的能量守恒，有：
联立解得：k=2
所以当k≤2时，两个滑块最终没有滑离小车．
4.
如图所示，在竖直平面内有一倾角θ=37°的传送带，两皮带轮AB轴心之间的距离L=3.2 m，沿顺时针方向以v0=2 m/s匀速运动．一质量m=2 kg的物块P从传送带顶端无初速度释放，物块P与传送带间的动摩擦因数μ=0.5．物块P离开传送带后在C点沿切线方向无能量损失地进入半径为
m的光滑圆弧形轨道CDF，并沿轨道运动至最低点F，与位于圆弧轨道最低点的物块Q发生碰撞，碰撞时间极短，物块Q的质量M ＝1 kg，物块P和Q均可视为质点，重力加速度g＝10 m/s2，sin 37°＝0.6，cos 37°＝0.8，．求：
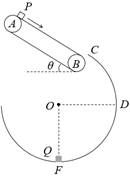
(1)物块P从传送带离开时的动量；
(2)传送带对物块P做功为多少；
(3)物块P与物块Q碰撞后瞬间，物块P对圆弧轨道压力大小的取值范围．
难度：
知识点：实验：验证动量守恒定律
使用次数：131
【答案】
(1)8kgm/s，方向与水平方向成
斜向右下；(2)-22.4J；(3)
【详解】
(1)物块在未到达与传送带共速之前,所受摩擦力方向沿传送带向下，
由牛顿第二定律得： 
解得
所需时间
沿斜面向下运动的位移
当物块
的速度与传送带共速后，由于 
，所以物块所受摩擦力方向沿传送带向上,由牛顿第定律得：
解得a2=2m/s2
物块以加速度
以运动的距离为：
设物块运动到传送带底端的速度为
,由运动学公式得v12=v02+2a2x2
解得
则动量为P=mv1=
，方向与水平方向成斜向右下
(2)物块从顶端到底端,根据动能定理：
可知传送带对物块做功为：W=
(3)设物块运动到
点的速度为
,由动能定理得
解得
若物块与物块
发生完全弹性碰撞，并设物块
碰撞后的速度为
,物块Q碰撞后的速度为
,则两物块的碰撞过程动量守恒，碰撞前后动能之和不变；
解得
若物块与物块发生完全非弹性碰撞,则
解得
所以物块的速度范围为：
在点由牛顿第二定律得：
解得：
物块碰撞后间对圆弧轨道的压力为
,由牛顿第三定律可得：
5.
如图所示，水平地面上静止放置一辆小车A，质量
，上表面光滑，小车与地面间的摩擦力极小，可以忽略不计．可视为质点的物块B置于A的最右端，B的质量
．现对A施加一个水平向右的恒力F＝10N，A运动一段时间后，小车左端固定的挡板B发生碰撞，碰撞时间极短，碰后A，B粘合在一起，共同在F的作用下继续运动，碰撞后经时间t＝0.6s，二者的速度达到
．求
（1）A开始运动时加速度a的大小；
（2）A，B碰撞后瞬间的共同速度v的大小；
（3）A的上表面长度l；
难度：
知识点：弹性碰撞和非弹性碰撞
使用次数：186
【答案】
(1)
（2）1m/s （3）0.45m
【详解】
(1)以A为研究对象，由牛顿第二定律有F＝mAa①
代入数据解得a＝2.5 m/s2②
(2)对A、B碰撞后共同运动t＝0.6 s的过程，由动量定理得Ft＝(mA＋mB)v－(mA＋mB)v1③
代入数据解得v1＝1 m/s④
(3)设A、B发生碰撞前，A的速度为vA，对A、B发生碰撞的过程，由动量守恒定律有
mAvA＝(mA＋mB)v1⑤
A从开始运动到与B发生碰撞前，由动能定理有Fl＝
mAv
⑥
由④⑤⑥式，代入数据解得l＝0.45 m.
本卷还有95题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
100
总体难度：
偏难
难度统计
难度系数
数量
占比
很难
5
5.0%
容易
16
16.0%
中等
50
50.0%
偏难
25
25.0%
基础
4
4.0%
题型统计
大题类型
数量
占比
解答题
20
20.0%
填空题
1
1.0%
选择题
28
28.00%
实验,探究题
51
51.0%
知识点统计
知识点
数量
占比
弹性碰撞和非弹性碰撞
13
13.0%
实验：验证动量守恒定律
36
36.0%
带电粒子在电场中的运动
1
1.0%
光的干涉
2
2.0%
动量守恒定律
6
6.0%
能量守恒定律
1
1.0%
反冲现象 火箭
3
3.0%
实验：用单摆测量重力加速度
19
19.0%
实验：用双缝干涉测量光的波长
18
18.0%
单摆
1
1.0%
版权提示
该作品由: 用户老客户分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。