2020湖北人教版(2019)高中物理专题练习120663
高中
整体难度：中等
2020-11-17
题号
一
二
三
四
五
评分
一、选择题 (共8题)
添加该题型下试题
1.
如图是世界物理学史上两个著名实验的装置图，下列有关实验的叙述正确的是
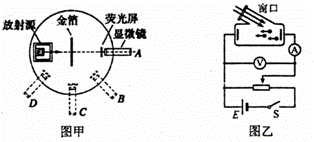
A．图甲是
粒子散射实验装置，卢瑟福指导他的学生们进行粒子散射实验研究时，发现了质子和中子
B．图甲是粒子散射实验装置，汤姆孙根据粒子散射实验，提出了原子“枣糕模型”结构
C．图乙是研究光电效应的实验装置，根据光电效应规律，超过极限频率的入射光频率越大，则光电子的最大初动能越大
D．图乙是研究光电效应的实验装置，根据光电效应规律，超过极限频率的入射光光照强度一定，则光的频率越大所产生的饱和光电流就越大
难度：
知识点：光电效应
使用次数：121
【答案】
C
【解析】
AB、图甲是粒子散射实验装置，卢瑟福提出了核式结构模型；卢瑟福通过用粒子轰击氮原子放出氢核，发现了质子；查得威克发现了中子；汤姆孙通过研究阴极射线中粒子的性质发现了电子，故选项A、B错误；
C、图乙是研究光电效应的实验装置，根据光电效应方程
可知超过极限频率的入射光频率越大，则光电子的最大初动能越大，故选项C正确；
D、光较强时，包含的光子数较多，照射金属时产生的光电子较多，因而饱和电流较大，入射光的光强一定时，频率越大，光电子的最大初动能最越大，而不是所产生的饱和光电流就越大，故选项D错误．
2.
如图所示，一光滑半圆形轨道固定在水平地面上，圆心为O、半径为R，一根轻橡皮筋一端连在可视为质点的小球上。另一端连在距离O点正上方R处的P点。小球放在与O点等高的轨道上A点时，轻橡皮筋处于原长。现将小球从A点由静止释放，小球沿圆轨道向下运动，通过最低点B时对圆轨道的压力恰好为零。已知小球的质量为m，重力加速度为g，则小球从A点运动到B点的过程中下列说法正确的是（ ）
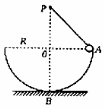
A．小球通过最低点时，橡皮筋的弹力等于mg
B．橡皮筋弹力做功的功率逐渐变大
C．小球运动过程中，橡皮筋弹力所做的功等于小球动能增加量
D．小球运动过程中，机械能的减少量等于橡皮筋弹性势能的增加量
难度：
知识点：生活中的圆周运动
使用次数：112
【答案】
D
【解析】
小球运动到最低点时，根据牛顿第二定律可得F-mg=m
，橡皮筋的弹力F=mg+m，故F大于mg，故A错误；根据P=Fvcosα可知，开始时v=0，则橡皮筋弹力做功的功率P=0．在最低点速度方向与F方向垂直，α=90°，则橡皮筋弹力做功的功率P=0，故橡皮筋弹力做功的功率先变大后变小，故B错误；小球运动过程中，根据动能定理知，重力做功和橡皮筋弹力所做的功之和等于小球动能增加量，故C错误。小球和弹簧组成的系统机械能守恒，知小球运动过程中，机械能的减少量等于橡皮筋弹性势能的增加量，故D正确。
3.
电磁流量计广泛应用于测量可导电流体（如污水）在管中的流量（在单位时间内通过管内横截面的流体的体积）。为了简化，假设流量计是如图所示的横截面为长方形的一段管道，其中空部分的长、宽、高分别为图中的a、b、c．流量计的两端与输送流体的管道相连接（图中虚线）。图中流量计的上下两面是金属材料，前后两面是绝缘材料。现于流量计所在处加磁感应强度为B的匀强磁场，磁场方向垂直于前后两面。当导电流体稳定地流经流量计时，在管外将流量计上、下两表面分别与一电压表（内阻很大）的两端连接，U表示测得的电压值。则可求得流量为（ ）
A．
B．
C．
D．
难度：
知识点：质谱仪与回旋加速器
使用次数：129
【答案】
A
【解析】
将流量计上、下两表面分别与一电压表（内阻很大）的两端连接，U表示测得的电压值，
那么电动势E＝U；根据粒子平衡得，
联立两式解得，
。则流量Q＝vS＝vbc＝ ．故A正确，BCD错误。
4.
一含有理想变压器的电路如图所示，交流电源输出电压的有效值不变，图中三个电阻R完全相同，电压表为理想交流电压表，当开关S断开时，电压表的示数为U0；当开关S闭合时，电压表的示数为
．变压器原、副线圈的匝数比为（ ）
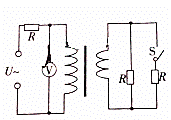
A．5 B．6 C．7 D．8
难度：
知识点：变压器
使用次数：172
【答案】
B
【解析】
设变压器原、副线圈匝数之比为k，当开关断开时，副线圈电压为
，根据欧姆定律得副线圈中电流为：
，则原线圈中电流为：
，则交流电的输出电压为：
①；当S闭合时，电压表的示数为，则副线圈的电压为
，根据欧姆定律得：
，则原线圈中电流为：
，则交流电的输出电压为：
②；①②联立解得k=6，故B正确．
5.
如图所示为鱼饵自动投放器的装置示意图，其下部是一个高度可以调节的竖直细管，上部是四分之一圆弧弯管，管口沿水平方向．竖直细管下端装有原长为L0的轻质弹簧，弹簧下端与水面平齐，将弹簧压缩并锁定，把鱼饵放在弹簧上．解除锁定当弹簧恢复原长时鱼饵获得速度v0．不考虑一切摩擦，重力加速度取g，调节竖直细管的高度，可以改变鱼饵抛出后落水点距管口的水平距离，则该水平距离的最大值为
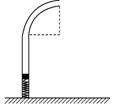
A．
＋L0 B．
＋2L0 C．－L0 D．－2L0
难度：
知识点：机械能守恒定律
使用次数：154
【答案】
A
【解析】
设弹簧恢复原长时弹簧上端距离圆弧弯管口的竖直距离为h，根据动能定理有－mgh=
，鱼饵离开管口后做平抛运动，竖直方向有h＋L0=
gt2，鱼饵被平抛的水平距离x=vt，联立解得
，所以调节竖直细管的高度时，鱼饵被投放的最远距离为＋L0，选项A正确．
本卷还有11题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
16
总体难度：
中等
难度统计
难度系数
数量
占比
中等
9
56.25%
容易
5
31.25%
很难
1
6.25%
偏难
1
6.25%
题型统计
大题类型
数量
占比
选择题
8
50.0%
实验,探究题
3
18.75%
解答题
4
25.0%
填空题
1
6.25%
知识点统计
知识点
数量
占比
光电效应
1
6.25%
生活中的圆周运动
1
6.25%
质谱仪与回旋加速器
1
6.25%
变压器
1
6.25%
机械能守恒定律
1
6.25%
带电粒子在电场中的运动
1
6.25%
曲线运动
1
6.25%
牛顿运动定律的应用
1
6.25%
动量守恒定律
1
6.25%
实验 练习使用多用电表
1
6.25%
实验 用油膜法估测油酸分子的大小
1
6.25%
动能和动能定律
1
6.25%
实验：验证动量守恒定律
1
6.25%
气体的等压变化和等容变化
1
6.25%
光的折射
1
6.25%
波的描述
1
6.25%
版权提示
该作品由: 用户王波分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。