2021人教版(2019)高中物理专题练习137830
高中
整体难度：中等
2020-10-19
题号
一
二
三
四
五
评分
一、计算题 (共14题)
添加该题型下试题
1.
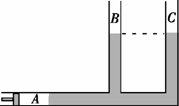
如图所示,导热性能良好的汽缸管道A、B、C横截面积相等,管道B、C中的水银柱高度均为24 cm,活塞与水银柱之间封闭了一段长度为60 cm的理想气柱,大气压强为76 cmHg。缓慢移动活塞,使管道B、C中的水银柱均上升20 cm,管道A中的空气没有进入管道B、C中。
(1)求该过程中,活塞移动的距离l。
(2)判断管道A中的气体是吸热还是放热,并说明理由。
难度：
知识点：气体的等温变化
使用次数：110
【答案】
(1)50 cm (2)放热 理由见解析
【解析】：(1)设活塞的横截面积为S,活塞移动后,气柱长为x,对于管道A中的气体
初状态:压强：
p1=76 cmHg+24 cmHg=100 cmHg...................................................................①
体积V1=60S............................................................................................................②
末状态:压强：
p2=76 cmHg+24 cmHg+20 cmHg=120 cmHg..................................................③
体积V2=x S.................................................................................................................④
由玻意耳定律有：
p1V1=p2V2............................................................................................................⑤
解得：x=50 cm
活塞向右移动的距离
d=60 cm-50 cm+20 cm+20 cm=50 cm...................................................................⑥
(2)根据热力学第一定律ΔU=W+Q,气体温度不变,ΔU=0,外界对气体做功,W>0,可得Q<0,故气体放热。
2.
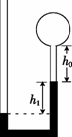
如图所示,竖直放置、粗细均匀且足够长的U形玻璃管与容积V0=8 cm3的金属球形容器连通,用U形玻璃管中的水银柱封闭一定质量的理想气体。当环境温度t1=27 ℃时,U形玻璃管右侧水银面比左侧水银面高出h1=15 cm,水银柱上方玻璃管中的空气柱长h0=4 cm。现在左管中加入水银,保持温度不变,使两边水银柱在同一高度。(已知大气压p0=75 cmHg,U形玻璃管的横截面积S=0.5 cm2)
(1)求需要加入的水银柱的长度l。
(2)若使右管水银面恢复到原来的位置,则封闭气体应加热到多少摄氏度?
难度：
知识点：气体的等温变化
使用次数：118
【答案】
(1)23 cm (2)142 ℃
【解析】：(1)以球形容器中的理想气体为研究对象,初状态压强：
p1=p0-15 cmHg.....................................................①
V1=V0+h0S.....................................................②
末状态：压强
p2=p0=75 cmHg.....................................................③
根据玻意耳定律有
p1V1=p2V2.....................................................④
解得：
V2=8 cm3.....................................................⑤
即水银正好到球的底部
加入的水银柱长度：
l=h1+2h0=23 cm.....................................................⑥
(2) 以球形容器中的理想气体为研究对象,初状态:压强
p1=p0-15 cmHg,温度T1=300 K.....................................................⑦
末状态:压强：
p3=p0+8 cmHg.....................................................⑧
设温度为T3
根据查理定律有：
.....................................................⑨
解得：
T3=415 K.....................................................⑩
即气体应加热到142 ℃。
3.
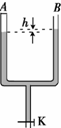
如图所示,一粗细均匀的U形管竖直放置,A侧上端封闭,B侧上端与大气相通,下端开口处开关K关闭;A侧空气柱的长度l=10.0 cm,B侧水银面比A侧的高h=3.0 cm。现将开关K打开,从U形管中放出部分水银,当两侧水银面的高度差h1=10.0 cm时将开关K关闭。已知大气压强p0=75.0 cmHg。
(1)求放出部分水银后A侧空气柱的长度。
(2)此后再向B侧注入水银,使A、B两侧的水银面达到同一高度,求注入的水银在管内的长度。
难度：
知识点：气体的等温变化
使用次数：195
【答案】
(1)12.0 cm (2)13.2 cm
【解析】：(1)以cmHg为压强单位。设A侧空气柱长度l=10.0 cm时压强为p,当两侧水银面的高度差h1=10.0 cm时,空气柱的长度为l1,压强为p1,由玻意耳定律,有：
plS=p1l1S..............................................................①
由平衡条件有：
p=p0+h..................................................................②
打开开关放出水银的过程中B侧水银面处的压强始终为p0,而A侧水银面处的压强随空气柱长度的增加逐渐减小,B、A两侧水银面的高度差也随着减小,直至B侧水银面低于A侧水银面h1为止,由平衡条件有：p1=p0-h1
联立解得：
l1=12.0 cm..............................................................③
(2)当A、B两侧的水银面达到同一高度时,设A侧空气柱的长度为l2,压强为p2,由玻意耳定律,有
plS=p2l2S..............................................................④
由平衡条件有p2=p0
联立解得：
l2=10.4 cm..............................................................⑤
设注入水银在管内的长度为Δh,依题意有
Δh=2(l1-l2)+h1..............................................................⑥
联立解得：
Δh=13.2 cm..............................................................⑦
4.
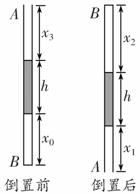
如图所示，一根粗细均匀的长l＝72 cm的细玻璃管AB开口朝上竖直放置，玻璃管中有一段长h＝24 cm 的水银柱，下端封闭了一段长x0＝24 cm的空气柱，系统温度恒定，外界大气压强恒为p0＝76 cmHg.现将玻璃管缓慢倒置，若空气可以看做理想气体，求倒置后水银柱相对B端移动的距离．
难度：
知识点：气体的等温变化
使用次数：119
【答案】
22 cm
【解析】：设水银密度为ρ，玻璃管横截面积为S，重力加速度为g.如图所示，倒置前，下部空气压强为：
pB＝p0＋ρgh＝100 cmHg ..........................................................................①
倒置后，若水银没有流出玻璃管，封闭空气柱的压强为：
p′＝p0－ρgh.................................................................................②
由玻意耳定律得：
pBSx0＝p′Sx2.................................................................................③
解得：
x2＝46 cm....................................................................................④
则x2＋h＜l，故假设成立
所以水银柱相对B端移动46 cm－24 cm＝22 cm..........................................................................⑤
5.
如图所示，竖直放置、粗细均匀的玻璃管开口向上，管里一段高为h=15cm的水银柱封闭一段长为L=14 cm的气体，水银柱的截面积为S，若将玻璃管按如图2所示倾斜放置，倾角为θ=37°，重力加速度g=10 m/s2，大气压强p0=75cmHg，sin 37°=0.6，cos 37°=0.8，求：
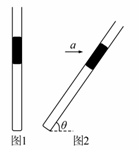
（ⅰ）倾斜后气柱的长度；
（ⅱ）如果将图2所示的玻璃管以一定的加速度向右加速运动，如果空气柱的长度又变成L，则加速度a为多大？
难度：
知识点：气体的等温变化
使用次数：171
【答案】
（ⅰ）x=15 cm （ⅱ）5 m/s2
【解析】（ⅰ）玻璃管竖直时，管内气体压强：
P1=75+15=90 cmHg.......................................................................................①
当玻璃管倾斜时，管内气体压强：
P2=P0+ρghsin37°=84cmHg................................................................................②
气体发生等温变化，则有：
P1LS=P2xS..........................................................................................................③
解得：
x=15cm..........................................................................................................④
（ⅱ）如果玻璃管向右做加速运动，使管中气体的长度仍为L，则管内气体的压强仍为P1，对水银柱研究，受力如图所示，有：
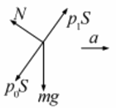
（P1–P0）Scos
–Nsin=ma ................................................................................⑤
（P1–P0）Ssin+Ncos=mg................................................................................⑥
其中：
m=ρSh ..................................................................................................⑦
解得：
a=0.5g=5m/s2................................................................................⑧
本卷还有9题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
14
总体难度：
中等
难度统计
难度系数
数量
占比
容易
2
14.28%
中等
11
78.57%
偏难
1
7.14%
题型统计
大题类型
数量
占比
计算题
14
100.0%
知识点统计
知识点
数量
占比
气体的等温变化
13
92.85%
气体的等压变化和等容变化
1
7.14%
版权提示
该作品由: 用户费宗杨分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。