下列说法中正确的是( )
A.石墨和金刚石是晶体,玻璃和橡胶是非晶体
B.同种元素形成晶体只能有一种排列规律
C.晶体的分子(或原子、离子)排列是有规则的
D.晶体有固定的熔点,非晶体没有固定的熔点
E.在物理性质上,所有晶体都具有各向异性,非晶体具有各向同性
ACD 晶体和非晶体.
【分析】物质结构决定物质性质,金刚石、石墨的内部结构不同,二者的物理性质不同,它们都是晶体;晶体有固定的熔点,非晶体没有固定的熔点;液晶的光学性质随外加电压的变化而变化.
【解答】解:A、金刚石、石墨都是由碳原子组成的,只是排列方式不同,导致两种物质物理性质差异很大,但它们都是晶体;玻璃、橡胶是非晶体.故A正确;
B、同种元素形成的晶体不一定具有相同的原子排列规律,比如碳元素,金刚石与石墨,故B错误;
C、晶体的分子(或原子、粒子)排列是有规则的,故C正确;
D、晶体有固定的熔点,非晶体没有固定的熔点,故D正确;
E、只有单晶体具有各向异性,而多晶体和非晶体则是各向同性的,故E错误;
故选:ACD
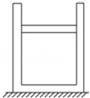
如图所示,一个内壁光滑的导热气缸竖直放置,内部封闭一定质量的理想气体,环境温度为27℃,现将一个质量为m=2kg的活塞缓慢放置在气缸口,活塞与气缸紧密接触且不漏气.已知活塞的横截面积为S=4.0×10﹣4m2,大气压强为P0=1.0×105Pa,重力加速度g取10m/s2,气缸高为h=0.3m,忽略活塞及气缸壁的厚度.
(i)求活塞静止时气缸内封闭气体的体积.
(ii)现在活塞上放置一个2kg的砝码,再让周围环境温度缓慢升高,要使活塞再次回到气缸顶端,则环境温度应升高到多少摄氏度?

理想气体的状态方程.
【分析】(1)气缸内的气体发生等温变化,列出初末状态参量,根据玻意耳定律列式求解;
(2)先求出放置砝码后封闭气体的压强,缓慢升温过程中,气体发生等压变化,根据盖﹣吕萨克定律即可求解;
【解答】解:(i)气缸内的封闭气体等温变化.将活塞放置在气缸口时,封闭气体的压强为:p1=1.0×105Pa,体积为:V1=Sh=1.2×10﹣4m3
活塞静止时,气缸内封闭气体的压强为:p2=p0+![]()
![]() =
=![]()
![]() =1.5×105Pa
=1.5×105Pa
根据玻意耳定律有:p1V1=p2V2
解得:V2=![]()
![]() =
=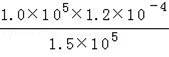
 =8×10﹣5m3
=8×10﹣5m3
(ii)放置砝码后,活塞再次静止时,封闭气体的压强为:
p'2=p0+![]()
![]() =
=![]()
![]() =2.0×105Pa
=2.0×105Pa
环境温度缓慢升高,活塞再次回到气缸顶端时,根据查理定律有: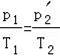

解得:T2=![]()
![]() =
=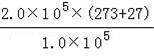
 =600 K
=600 K
故此时环境温度为:t=℃=327℃
答:(i)活塞静止时气缸内封闭气体的体积为![]()
![]()
(ii)现在活塞上放置一个2kg的砝码,再让周围环境温度缓慢升高,要使活塞再次回到气缸顶端,则环境温度应升高到327摄氏度
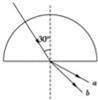
如图,某种复合光经过半圆形的玻璃砖后分成a、b两束,其中光束a与法线的夹角为60°,光束b与法线的夹角为45°,则玻璃对a、b两种光的折射率之比na:nb= ;若a、b两种光在这种玻璃中的波长之比为![]()
![]() :
:![]()
![]() ,现用同一双缝干涉装置分别测量a、b两种光的波长,则得到的相邻亮条纹间距之比为△xa:△xb= .
,现用同一双缝干涉装置分别测量a、b两种光的波长,则得到的相邻亮条纹间距之比为△xa:△xb= .

光的折射定律.
【分析】根据折射定律求出折射率之比.由v=![]()
![]() 和波速公式v=λf求出光在真空中波长之比,从而求得相邻亮条纹间距之比.
和波速公式v=λf求出光在真空中波长之比,从而求得相邻亮条纹间距之比.
【解答】解:由光的折射定律 n=![]()
![]() 分别得出 na=
分别得出 na=![]()
![]() =
=![]()
![]() ,nb=
,nb=![]()
![]() =
=![]()
![]() ,所以na:nb=
,所以na:nb=![]()
![]() :
:![]()
![]() ;
;
设光在真空中和介质中波长分别为λ0和λ,则:
在真空中有 c=λ0f
在介质中有 v=λf
又 v=![]()
![]() ,则得 λf=
,则得 λf=![]()
![]()
故真空中的波长λ0=nλ,所以 ![]()
![]() =
=![]()
![]() •
•![]()
![]()
据题:a、b两种光在这种玻璃中的波长之比为 ![]()
![]() =
=![]()
![]()
所以可行,a、b两种光在真空中的波长之比为 ![]()
![]() =
=![]()
![]()
根据△x=![]()
![]() 得:相邻亮条纹间距之比为△xa:△xb=λ0a:λ0b=3:2
得:相邻亮条纹间距之比为△xa:△xb=λ0a:λ0b=3:2
故答案为:![]()
![]() :
:![]()
![]() ,3:2
,3:2
如图所示为一列沿x轴正方向传播的简谐横波在t=0时刻的波形图,已知该波的传播速度为6.4m/s,求: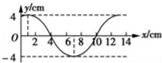

(i)这列波的周期;
(ii)平衡位置在x=4cm处的质点在0~0.05s时间内运动的路程.
波长、频率和波速的关系;横波的图象.
【分析】(i)根据波形图读出波长,再由v=![]()
![]() 求出周期;
求出周期;
(ii)根据质点的周期,由0.05s 算出完成多少个全振动,从而由振幅来确定x=4cm处质点在这段时间内运动的路程.
【解答】解:(i)由题图可知波长 λ=12 cm=0.12m
则周期 T=![]()
![]() =
=![]()
![]() =
=![]()
![]() s
s
(ii)质点从平衡位置出发一个周期运动4A,半个周期运动2A,平衡位置在x=4 cm处的质点从平衡位置开始运动
△t=0.05 s=2![]()
![]() T=2T+
T=2T+![]()
![]() T+
T+![]()
![]() T
T
由题图知,x=4 cm处的质点的振动方程为y=Asinωt=Asin![]()
![]() t
t
故在最后![]()
![]() T时间内质点运动的路程是Asin (
T时间内质点运动的路程是Asin (![]()
![]() •
•![]()
![]() T)=
T)=![]()
![]() A
A
所以总的路程是2.5×4A+![]()
![]() A=(10×4+
A=(10×4+![]()
![]() ×4)cm=
×4)cm=![]()
![]() m.
m.
答:
(i)这列波的周期是![]()
![]() s;
s;
(ii)平衡位置在x=4cm处的质点在0~0.05s时间内运动的路程是![]()
![]() m.
m.
如图所示,质量为m=2kg的物块A从高为h=0.2m的光滑固定圆弧轨道顶端由静止释放,圆弧轨道底端的切线水平,物块A可从圆弧轨道的底端无能量损失地滑上一辆静止在光滑水平面上的小车B,且物块A恰好没有滑离小车B.已知小车B的长度为l=0.75m,质量M=6kg,重力加速度为g=10m/s2,求:
(1)物块A与小车B间的动摩擦因数;
(2)当物块A相对小车B静止时小车B运动的位移.
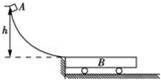

动量守恒定律;动能定理的应用.
【分析】(1)根据动能定理求出物块A运动到圆弧轨道底端时的速度.物块A在小车B上运动时,由动量守恒定律和能量守恒定律结合求解物块A与小车B间的动摩擦因数;
(2)对B,运用动能定理或牛顿第二定律和运动学公式结合求解小车B运动的位移.
【解答】解:(1)设物块A从圆弧轨道顶端滑到底端时的速度为v0,由动能定理可得:
mgh=![]()
![]()
解得:v0=![]()
![]() =
=![]()
![]() =2 m/s
=2 m/s
物块A滑上小车B后,系统动量守恒,设它们相对静止时的速度为v,取向右为正方向,由动量守恒定律得:
mv0=(m+M)v
代入数据解得:v=0.5 m/s
由能量守恒定律可得:
![]()
![]() =
=![]()
![]() (m+M)v2+μmgl
(m+M)v2+μmgl
解得 μ=0.2
(2)物块A滑上小车B后,小车B做匀加速运动,小车B的加速度为:a=![]()
![]() =
=![]()
![]() =
=![]()
![]() m/s2
m/s2
它们相对静止时,小车运动的位移为:xB=![]()
![]() =
=![]()
![]() =
=![]()
![]() m.
m.
答:(1)物块A与小车B间的动摩擦因数是0.2;
(2)当物块A相对小车B静止时小车B运动的位移是![]()
![]() m.
m.
本卷还有1题,登录并加入会员即可免费使用哦~

该作品由: 用户xiaohu分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。