2003上海人教版高中物理高考真题2305
高中
整体难度：容易
2009-03-14
题号
一
二
三
四
五
评分
一、计算题 (共4题)
添加该题型下试题
1.
为研究静电除尘，有人设计了一个盒状容器，容器侧面是绝缘的透明有机玻璃，它的上下底面是面积A＝0.04m2的金属板，间距L＝0.05m，当连接到U＝2500V的高压电源正负两极时，能在两金属板间产生一个匀强电场，如图所示，现把一定量均匀分布的烟尘颗粒密闭在容器内，每立方米有烟尘颗粒1013个，假设
这些颗粒都处于静止状态，每个颗粒带电量为q＝+1.0×10－17C，质量为m＝2.0×10－15kg，不考虑烟尘颗粒之间的相互作用和空气阻力，并忽略烟尘颗粒所受重力。
求合上电键后：
（1）经过多长时间烟尘颗粒可以被全部吸附？
（2） 除尘过程中电场对烟尘颗粒共做了多少功？
（3）经过多长时间容器中烟尘颗粒的总动能达到最大？
难度：
知识点：带电粒子在电场中的运动
使用次数：112
【答案】
解：（1）当最靠近上表面的烟尘颗粒被吸附到下板时，烟尘就被全部吸附烟尘颗粒受到的电场力
∴
（2）
＝2.5×10－4（J）
（3）设烟尘颗粒下落距离为
，
当
时，
达最大， 
2.
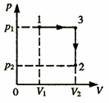如图所示，1、2、3为p-V图中一定量理想气体的三个状态，该理想气体由状态1经过程1-3-2到达状态2。试利用气体实验定律证明：
难度：
知识点：气体的等温变化
使用次数：144
【答案】
解：设状态3的温度为T 1-3为等压过程 
3-2为等容过程 
消去T即得 
3.
质量为m的飞机以水平速度v0飞离跑道后逐渐上升，若飞机在此过程中水平速度保持不变，同时受到重力和竖直向上的恒定升力（该升力由其它力的合力提供，不含重力）。今测得当飞机在水平方向的位移为l时，它的上升高度为h，求：（1）飞机受到的升力大小；（2）从起飞到上升至h高度的过程中升力所作的功及在高度h处飞机的动能。
难度：
知识点：专题四 功和能
使用次数：181
【答案】
解：（1）飞机水平速度不变 
y方向加速度恒定 
消去t即得 
由牛顿第二定律 
（2）升力做功 
在h处 
∴ 
4.
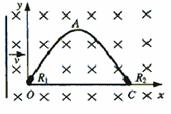
如图所示，OACO为置于水平面内的光滑闭合金属导轨，O、C处分别接有短电阻丝（图中粗线表法），R1＝4Ω、R2＝8Ω（导轨其它部分电阻不计）。导轨OAC的形状满足方程
（单位：m）。磁感强度B＝0.2T的匀强磁场方向垂直于导轨平面。一足够长的金属棒在水平外力F作用下，以恒定的速率v＝5.0m/s水平向右在导轨上从O点滑动到C点，棒与导思接触良好且始终保持与OC导轨垂直，不计棒的电阻。
求：（1）外力F的最大值；
（２）属棒在导轨上运动时电阻丝R1上消耗的最大功率；
（3）在滑动过程中通过金属棒的电流I与时间t的关系。
难度：
知识点：电磁感应单元测试
使用次数：97
【答案】
解：（1）金属棒匀速运动 
I＝ε/R总
F外＝BIL＝B2L2v/R总
∴ 
（2）
（3）金属棒与导轨接触点间的长度随时间变化
且
，
∴ 
二、选择题 (共4题)
添加该题型下试题
本卷还有8题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
13
总体难度：
容易
难度统计
难度系数
数量
占比
中等
5
38.46%
基础
7
53.84%
容易
1
7.69%
题型统计
大题类型
数量
占比
计算题
4
30.76%
选择题
4
30.76%
多项选择
3
23.07%
实验,探究题
2
15.38%
知识点统计
知识点
数量
占比
带电粒子在电场中的运动
1
7.69%
核裂变与核聚变
1
7.69%
机械波单元测试
1
7.69%
光电效应
1
7.69%
专题四 功和能
2
15.38%
未分类
2
15.38%
抛体运动的规律
1
7.69%
气体的等温变化
2
15.38%
电磁感应单元测试
1
7.69%
原子的核实结构模型
1
7.69%
版权提示
该作品由: 用户重新爱分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。