两根相距d=0.20米的平行金属长导轨固定在同一水平面内,并处于竖直方向的匀强磁场中,磁场的磁感应强度B=0.2特,导轨上面横放着两条金属细杆,构成矩形回路,每条金属细杆的电阻为r=0.25欧,回路中其余部分的电阻可不计.已知两金属细杆在平行于导轨的拉力的作用下沿导轨朝相反方向匀速平移,速度大小都是v=5.0米/秒,如图13所示.不计导轨上的摩擦.
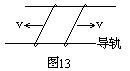
(1)求作用于每条金属细杆的拉力的大小.
(2)求两金属细杆在间距增加0.40米的滑动过程中共产生的热量.
解:(1)当两金属杆都以速度v匀速滑动时,每条金属杆中产生的感应电动势分别为
ε1=ε=Bdv ①由闭合电路的欧姆定律,回路中的电流强度因拉力与安培力平衡,作用于每根金属杆的拉力的大小为 F1=F2=IBd ③由①②③式并代入数据得(2)设两金属杆之间增加的距离为△L,则两金属杆共产生的热量代入数据得 Q=1.28×10-2焦
将一个矩形金属线框折成直角框架abcdefa,置于倾角为α37°的斜面上,ab与斜面的底线MN平行,如图所示。ab=bc=cd=de=ef=fd=0.2米,线框总电阻为R=0.02欧,ab边和de边的质量均为m=0.01千克,其余四边的质量忽略不计。框架可绕过c、f点的固定轴转动。现从t=0时刻开始沿斜面向上加一随时间均匀增加的、范围足够大的匀强磁场,磁感强度与时间的关系为B=0.5t特,磁场方向与cdef面垂直 。
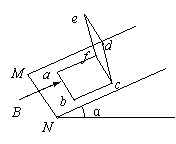
(1)求线框中感应电流的大小,并在ab段导线上画出感应电流的方向。
(2)t为何值时框架将开始绕其固定轴转动? (cos37°=0.8,sin30°=0.6,g=10米/秒2)
(1)ε=0.02(伏)

I=1.0(安),方向从a到b
(2)fab=0.1t,方向垂直斜面向上
Mf=fab・bc=0.02 t
MG=mg・bc・cosα+mg・cd・sinα=mg・bc・(cosα+sinα)=0.028(牛・米)
令Mf=mG,0.02t=0.028,t=1.4(秒)
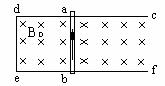
如图所示,固定于水平桌面上的金属框架cdef,处在竖直向下的匀强磁场中,金属棒ab搁在框架上,可无摩擦滑动。此时adeb构成一个边长为l的正方形。棒的电阻为r,其余部分电阻不计。开始时磁感强度为B0。

(1)若从t=0时刻起,磁感强度均匀增加,每秒增加为k,同时保持棒静止。求棒中的感应电流。在图上标出感应电流的方向。
(2)在上述(1)情况中,始终保持静止,当t=t1秒末时需加的垂直于棒的水平拉力为多大?
(3)若从t=0时刻起,磁感强度逐渐减小,当棒以恒定速度v向右作匀速运动时,可使棒中不产生感应电流,则磁感强度应怎样随时间变化(写出B与t的关系式)?
(1)感应电动势![]() ①
①
感应电流![]() ②
②
方向如图:逆时针方向
(2)t=t1秒时,B=B0+kt1 ③F=Blv ④
所以![]() ⑤总磁通量不变Bl(l+vt)=B0l2 ⑥所以
⑤总磁通量不变Bl(l+vt)=B0l2 ⑥所以![]()
![]() ⑦
⑦
一平面线圈用细杆悬于P点,开始时细杆处于水平位置,释放后让它在如图所示的匀强磁场中运动。已知线圈平面始终与纸面垂直,当线圈第一次通过位置Ⅰ和位置Ⅱ时,顺着磁场的方向看去,线圈中感应电流的方向分别为( )。

位置Ⅰ 位置Ⅱ
(A)逆时针方向 逆时针方向
(B)逆时针方向 顺时针方向
(C)顺时针方向 顺时针方向
(D)顺时针方向 逆时针方向
B
右图中abcd为一边长为l、具有质量的刚性导线框,位于水平面内,bc边中串接有电阻R,导线的电阻不计。虚线表示一匀强磁场区域的边界,它与线框的ab边平行。磁场区域的宽度为2l,磁感应强度为B,方向竖直向下。线框在一垂直于ab边的水平恒定拉力作用下,沿光滑水平面运动,直到通过磁场区域。已知ab边刚进入磁场时,线框便变为匀速运动,此时通过电阻R的电流的大小为i0,试在右图的i-x坐标上定性画出:从导线框刚进入磁场到完全离开磁场的过程中,流过电阻R的电流i的大小随ab边的位置坐标x变化的曲线。

x (0→l) i=i0
(l→2l) i=0
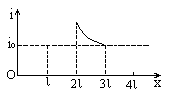
(2l→3l)如图,且x=3l处i≥I0
本卷还有2题,登录并加入会员即可免费使用哦~

该作品由: 用户小小分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。