∴设抛物线解析式为。

根据题意，得，解得。

∴抛物线的解析式为。

由，得D点坐标为（1，4），对称轴为。

①若以CD为底边，则PD=PC，

设P点坐标为，根据勾股定理，得

，

即。

又点P在抛物线上，

∴，即。

解得。

∵，应舍去，∴。

。

即点P的坐标为。

②若以CD为一腰，因为点P在对称轴右侧的抛物线上，由抛物线对称性知，

点P与点C关于直线对称，此时P点坐标为（2，3）。

∴符合条件的点P坐标为或（2，3）。

（2）由B（3，0），C（0，3），D（1，4），根据勾股定理，得

，,。

∴

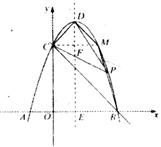
∴∠BCD=90º，

设对称轴交轴于点E，过C做CM⊥DE，交抛物线于点M，垂足为F。

在Rt△DCF中，

∵CF=DF=1，∴∠CDF=45º，

由抛物线的对称性知，

∠CDM=2×45º=90º，点M坐标为（2，3）

∴DM∥BC。

∴四边形BCDM为直角梯形。

由∠BCD=90º及题意可知，

以BC为一底时，顶点M在抛物线上的直角梯形只有上述一种情况；

以CD为一底或以BD为一底，且顶点M在抛物线上的直角梯形均不存在。

综上所述，符合条件的点M的坐标为（2，3）。