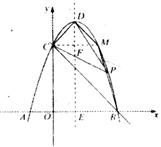
已知抛物线与x轴交于点A（-1,0），B（3,0）两点，与y轴交于点C（0,3）

（1）设抛物线的顶点为D，则在其对称轴右侧的抛物线上是否存在点P，使△PDC是等腰三角形？若存在，求出符合条件的点P的坐标；若不存在，请说明理由；

（2）若点M是抛物线上一点，以B 、C、D、M为顶点的四边形是直角梯形，试求出点M的坐标。

∴设抛物线解析式为。

根据题意，得，解得。

∴抛 物线的解析式为。

由，得D点 坐标为（1，4），对称轴为。

①若 以CD为底边，则PD=PC，

设P点坐标为，根据勾股定理，得

，

即。

又点P在抛物线上，

∴，即。

解得。

∵，应舍去，∴。

。

即 点P的坐标为。

②若以CD为一 腰，因为点P在对称轴右侧的抛物线上，由抛物线对称性知，

点P与 点C关于直线对称，此时P点 坐标为（2，3）。

∴符合条件的点P坐 标为或（2，3）。

（2）由B（3，0），C（0，3），D（1，4）， 根据勾股定理，得

，,。

∴

∴∠BCD=90º，

设对称轴交轴于点E， 过C做CM⊥DE， 交抛物线于点M，垂足为F。

在Rt△DCF中，

∵CF=DF=1，∴∠CDF=45º，

由抛物线的对称性知，

∠CDM=2×45º=90º， 点M坐标为（2，3）

∴DM∥BC。

∴四边形BCDM为 直角梯形。

由∠BCD=90º及 题意可知，

以BC为 一底时，顶点M在抛物线上的直角梯形只有上述一种情况；

以CD为一底或以BD为 一底，且顶点M在抛物线上的直角梯形均不存在。

综上所述，符合条件的点M的坐标为（2，3）。